---

In this lab you implement the intersection and ensure that all your code works properly within a graphical application.

---

1. Ensure that you have the necessary graphics files

   Microsoft Windows.

   Whether you are working on your own computer or a lab workstation, download the file SGL.zip. (You can right click on the link to download the file.) Once downloaded, unzip this file in the C:\ folder. Follow the instructions we shared in class for setting up your Visual Studio project. The class was recorded, so you can watch the video to remind yourself of the details.

   macOS. If you are running macOS, download the file SGL.zip, unzip it, and add both the sgl.h and sgl.hpp header files to your project. You also will need to configure your IDE to build your program with the OpenGL and GLUT frameworks. If you are using XCode or Visual Studio Code, inquire in lab about how to do this. We even may be able to figure out how to make it work if you are using a different IDE on your Mac. In the worst case, we always can compile from the Terminal if you have the XCode build tools installed (which you should have if you have a C++ compiler).

   Linux. If you are running Linux, inquire in lab for detailed installation instructions.

2. Create a new project

   Copy your geometry.h and geometry.cpp files into this new project. You will not be using the testgeom.cpp from before; instead, add visualgeometry.cpp to your project. This file contains the main function and all the necessary code to manage the graphics display. You should not modify the contents of visualgeometry.cpp.

3. Implement a new function

   You need to implement the intersection function that expects four double value parameters and two double reference parameters. Its prototype is

   void intersection(double m1, double b1, double m2, double b2, double& x, double& y);

   The function assigns to x and y the coordinates of the point of intersection of line #1 (slope = m1, intercept = b1) and line #2 (slope = m2, intercept = b2). Ordinarily the intercept component is the y-intercept, but note that if the slope of a line is INFINITY, the line is vertical and so its intercept represents an x-intercept rather than an y-intercept.

   If the lines do not have a single point of intersection, the function should assign INFINITY (declared in <cmath>) to both x and y. The client code then can check for a valid intersection point.

   How do you compute the point of intersection of two lines?

   • If the two lines have the same slope, there is no single point of intersection. The function assigns the bogus point (INFINITY, INFINITY) in that case.
   • If neither line is vertical, we have a pair of equations that look like y = m₁x + b₁
     y = m₂x + b₂ Since both righthand expressions equal y, set them equal to each other: m₁x + b₁ = m₂x + b₂ and solve for x:

     m1x - m2x + b1	=	m2x - m2x + b2
     m1x - m2x + b1	=	b2
     m1x - m2x + b1 - b1	=	b2 - b1
     m1x - m2x	=	b2 - b1
     (m1 - m2)x	=	b2 - b1
     x	=	(b2 - b1)/ (m1 - m2)

     This final equation

     x = (b₂ - b₁)/ (m₁ - m₂)

     serves as a formula to compute x. (In the C++ code you write you need only be concerned with this final formula.) Once you have x you can plug it into either of the original equations to compute y. This (x,y) point is the point of intersection of the two lines.

   • If one of the lines is vertical, you cannot use the above formula. Attempting to perform arithmetic with INFINITY will not produce a useful result. Since you know the x-intercept of the vertical line, you can deduce the x coordinate of the intersection directly from the vertical line. You then can plug this x value into the equation for the non-vertical line to compute the intersection point's y coordinate.

     Be sure that your code works correctly whether it be the first line or the second line that is vertical.

   Your intersection function must contain conditional logic to decide amongst the possibilities listed above.

4. Strategy

   The intersection function stub provided for you simply does nothing. Before you implement the intersection function ensure that the visualgeometry.cpp program builds without errors and executes without crashing. It should allow the user to add points and move them around. If the program does not allow the user to perform this minimal interaction, there may be lingering subtle errors in your geometry.cpp code. Until you correctly implement the intersection function, the lines will not draw properly. You should, however, be able to interact with the program without it crashing.

   Keep things simple to begin with, and implement the typical case that does not involve vertical lines. Once you can see the red intersection point of the two line segments, then you should proceed to the case that involves vertical lines. In order for the application to extend the lines to the edges of the window, it must be able to compute the lines' intersection points with the imaginary lines that make up the horizontal edges of the window (y = 100 and y = –100) or the vertical edges of the window (x = 100 and x = –100). It calls your intersection function to compute these points. This is why the application cannot render the extended lines completely until you correctly implement the intersection function.

   In the course of using the graphical application you may discover problems with one or more of your previous slope, intercept, and print_line functions that the handful of tests with testgeom.cpp did not reveal. You should repair any problems you discover.

5. Additional remarks

   You may have to fix errors in your existing functions if the new graphical client code reveals logic errors that were not uncovered by earlier tests.

   The most common problem is an incorrect and/or incomplete intersection function. The code within visualgeometry.cpp depends on a correctly written intersection function to draw a line from one side of the window to the other. Since it is easy to experiment with all kinds of lines visually, your testing may reveal errors in your existing code. If you do not see any lines or lines are missing in certain situations, focus on correcting your intersection function. Pay particular attention to how you handle vertical lines.

6. Program execution

   The graphical application allows the user to interactively supply points for lines that potentially intersect.

   

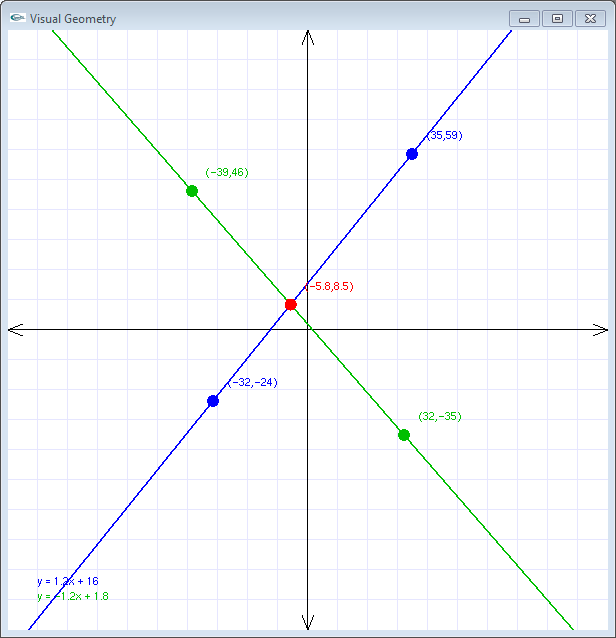
   The axes range from -100 to +100, so each square on the graph paper is 10 units wide by 10 units high. The location of the points, the equations of the lines, and the intersection point are printed in the console window. You do not need to program this functionality; it is built into visualgeometry.cpp. Remember, the only file you are supposed to touch is geometry.cpp; do not modify geometry.h or visualgeometry.cpp.

   Some useful interface shortcuts include:

   • If you wish wish to make a vertical line immediately, hold down the [Alt] key when placing the first point of the line. The graphical interface will automatically position the line's second point on the x-axis to create a vertical line.

   • If you wish wish to make a horizontal line immediately, hold down the [Ctrl] key when placing the first point of the line. The graphical interface will automatically position the line's second point on the y-axis to create a vertical line.

   • If you wish wish to clear all the points from the graph and make two new lines, press the [Esc] key.

7. Check out

   Your finished program will be evaluated for correctness and compliance. When approved, you should submit your geometry.cpp C++ source file to eclass.e.southern.edu. Be sure your name is included in a comment at the top of the source file.